LC: 1136. Parallel Courses

https://leetcode.com/problems/parallel-courses/

1136. Parallel Courses

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei.

In one semester, you can take any number of courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.

Return the minimum number of semesters needed to take all courses. If there is no way to take all the courses, return -1.

Example 1:

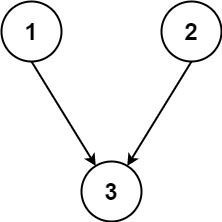
Input: n = 3, relations = [[1,3],[2,3]]
Output: 2
Explanation: The figure above represents the given graph.
In the first semester, you can take courses 1 and 2.
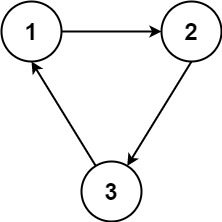
In the second semester, you can take course 3.

Example 2:

Input: n = 3, relations = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: No course can be studied because they are prerequisites of each other.

Constraints:

1 <= n <= 5000
1 <= relations.length <= 5000
relations[i].length == 2
1 <= prevCoursei, nextCoursei <= n
prevCoursei != nextCoursei
All the pairs [prevCoursei, nextCoursei] are unique.

Details:

The required solution is procedure is topological sorting. This can be achieved using Kahn's algorithm with BFS, which goes over individual layers. It can also be implemented using DFS, which is further useful to apply here because only maximum search depth is needed, not the actual sorting order.

Solution(s) and Further Explanation:

1136. Parallel Courses by ErdemT09 · Pull Request #180 · spiralgo/algorithmsGitHub

Default Code:

class Solution {
    public int minimumSemesters(int n, int[][] relations) {
        
    }
}

PreviousLC: 1135. Connecting Cities With Minimum-Cost NextLC: 1150. Check If a Number Is Majority Element in a Sorted Array

Last updated 4 years ago