LC: 1168. Optimize Water Distribution in a Village

Question

1168. Optimize Water Distribution in a Village

There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.

For each house i, we can either build a well inside it directly with cost wells[i - 1] (note the -1 due to 0-indexing), or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes, where each pipes[j] = [house1j, house2j, costj] represents the cost to connect house1j and house2j together using a pipe. Connections are bidirectional.

Return the minimum total cost to supply water to all houses.

Example 1:

Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
Output: 3
Explanation: 
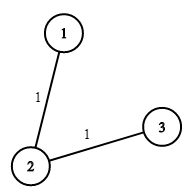
The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.

Example 2:

Input: n = 2, wells = [1,1], pipes = [[1,2,1]]
Output: 2

Constraints:

• 2 <= n <= 104

• wells.length == n

• 0 <= wells[i] <= 105

• 1 <= pipes.length <= 104

• pipes[j].length == 3

• 1 <= house1j, house2j <= n

• 0 <= costj <= 105

• house1j != house2j

The Essence

Details and Solutions