LC: 750. Number Of Corner Rectangles

https://leetcode.com/problems/number-of-corner-rectangles/

Question

Given an m x n integer matrix grid where each entry is only 0 or 1, return the number of corner rectangles.

A corner rectangle is four distinct 1's on the grid that forms an axis-aligned rectangle. Note that only the corners need to have the value 1. Also, all four 1's used must be distinct.

Example 1:

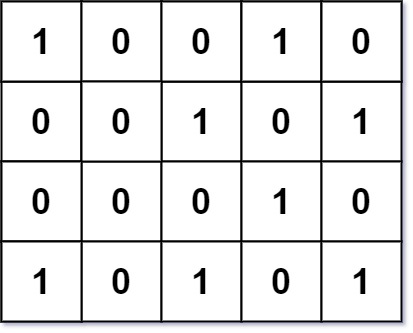
Input: grid = [[1,0,0,1,0],[0,0,1,0,1],[0,0,0,1,0],[1,0,1,0,1]]
Output: 1
Explanation: There is only one corner rectangle, with corners grid[1][2], grid[1][4], grid[3][2], grid[3][4].

Example 2:

Input: grid = [[1,1,1],[1,1,1],[1,1,1]]
Output: 9
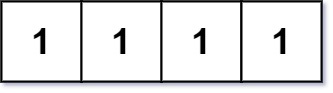
Explanation: There are four 2x2 rectangles, four 2x3 and 3x2 rectangles, and one 3x3 rectangle.

Example 3:

Input: grid = [[1,1,1,1]]
Output: 0
Explanation: Rectangles must have four distinct corners.

Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 200

• grid[i][j] is either 0 or 1.

• The number of 1's in the grid is in the range [1, 6000].

The Essence

Details and Solutions