LC: 296. Best Meeting Point

https://leetcode.com/problems/best-meeting-point/

Question

296. Best Meeting Point

Given an m x n binary grid grid where each 1 marks the home of one friend, return the minimal total travel distance.

The total travel distance is the sum of the distances between the houses of the friends and the meeting point.

The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.

Example 1:

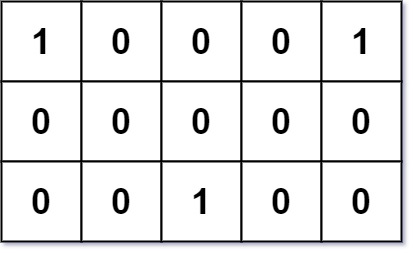
Input: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 6
Explanation: Given three friends living at (0,0), (0,4), and (2,2).
The point (0,2) is an ideal meeting point, as the total travel distance of 2 + 2 + 2 = 6 is minimal.
So return 6.

Example 2:

Input: grid = [[1,1]]
Output: 1

Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 200

• grid[i][j] is either 0 or 1.

• There will be at least two friends in the grid.

The Essence

Details and Solutions