LC: 276. Paint Fence

https://leetcode.com/problems/paint-fence/

Question

276. Paint Fence

You are painting a fence of n posts with k different colors. You must paint the posts following these rules:

• Every post must be painted exactly one color.

• There cannot be three or more consecutive posts with the same color.

Given the two integers n and k, return the number of ways you can paint the fence.

Example 1:

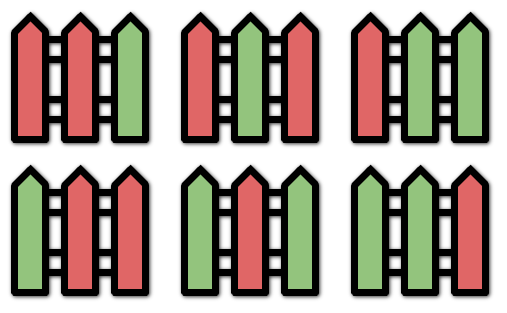
Input: n = 3, k = 2
Output: 6
Explanation: All the possibilities are shown.
Note that painting all the posts red or all the posts green is invalid because there cannot be three posts in a row with the same color.

Example 2:

Input: n = 1, k = 1
Output: 1

Example 3:

Input: n = 7, k = 2
Output: 42

Constraints:

• 1 <= n <= 50

• 1 <= k <= 105

• The testcases are generated such that the answer is in the range [0, 231 - 1] for the given n and k.

The Essence

Details and Solutions